A) Since tstat is inside the critical ±9.925 boundaries, we can't reject the β = 0 null hypothesis.
B) Since tstat is outside the critical ±9.925 boundaries, we can reject the β = 0 null hypothesis.
C) Since tstat is inside the critical ±7.845 boundaries, we can't reject the β = 0 null hypothesis.
D) Since tstat is inside the critical ±7.845 boundaries, we can reject the β = 0 null hypothesis.
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Application of the least squares criterion to regression analysis results in values of the y intercept and the slope that minimizes the sum of the squared deviations between the:
A) observed values of x and the estimated values of y
B) observed values of y and the estimated values of x
C) observed values of the dependent variable and the estimated values of the dependent variable
D) observed values of the independent variable and the estimated values of the independent variable
E) none of the above
G) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The following data have been collected for a simple linear regression analysis.  The least squares line would predict a y value of _______ for an x value of 15.
The least squares line would predict a y value of _______ for an x value of 15.
A) 16.2
B) 21.4
C) 20.9
D) 19.3
E) 18.1
G) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The manager of a local shopping mall uses simple linear regression to develop an equation that predicts the number of daily shoplifting incidents at the mall's stores based on the number of security guards employed.The manager uses the following data:  The slope of the regression line is b = -1.2; the intercept of the regression line is a = 14.5.
Conduct a hypothesis test to determine whether you can reject the null hypothesis that the population slope, β, is 0 at a 5% significance level.Compute the value of the sample test statistic, tstat.Which of the following is the correct conclusion?
The slope of the regression line is b = -1.2; the intercept of the regression line is a = 14.5.
Conduct a hypothesis test to determine whether you can reject the null hypothesis that the population slope, β, is 0 at a 5% significance level.Compute the value of the sample test statistic, tstat.Which of the following is the correct conclusion?
A) Since tstat is outside the critical values of ±3.182, we can reject the β=0 null hypothesis.
B) Since tstat is outside the critical values of ±4.303, we can reject the β=0 null hypothesis.
C) Since tstat is not outside the critical values of ±3.182, we cannot reject the β=0 null hypothesis.
D) Since tstat is not outside the critical values of ±4.303, we cannot reject the β=0 null hypothesis.
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Which of the following best describes the least squares criterion?
A) it identifies the best fitting line as the line that minimizes the sum of the squared vertical distances of points from the line
B) the best fitting line minimizes the sum of the horizontal distances from the line
C) it minimizes the sum of the absolute distances from the line
D) it is a measure of the goodness of fit of the estimated regression equation
E) none of the above
G) B) and C)
Correct Answer

verified
Correct Answer
verified
True/False
The standard error of estimate (sy.x) in simple linear regression is the square of the Mean Square Error (MSE) which is the sum of squares error (SSE) multiplied by its degrees of freedom n-2.
B) False
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The following data have been collected for a simple linear regression analysis relating sales (y) to price (x) :  In applying the least squares criterion, the slope (b) and the intercept (a) for the best-fitting line are b = -12 and a = 162.You are to conduct a hypothesis test to determine whether you can reject the null hypothesis that the population slope, β, is 0 at the 1% significance level.Report the value of the appropriate sample test statistic, tstat.
In applying the least squares criterion, the slope (b) and the intercept (a) for the best-fitting line are b = -12 and a = 162.You are to conduct a hypothesis test to determine whether you can reject the null hypothesis that the population slope, β, is 0 at the 1% significance level.Report the value of the appropriate sample test statistic, tstat.
A) -2.27
B) -1.23
C) -4.16
D) -3.52
E) -3.01
G) A) and C)
Correct Answer

verified
Correct Answer
verified
True/False
A procedure used for finding the equation of a straight line that provides the best fit for the relationship between the independent and dependent variables is called the minimum deviations method.
B) False
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Economist Joshua Grant is using linear regression to try to establish a link between the unemployment rate (x) and monthly home sales in the region (y) .The following data are available: 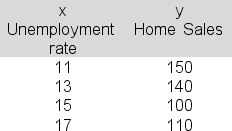 The slope term (b) in the estimated regression equation is -8.The intercept term (a) is 237.Construct a 95% confidence interval estimate of E(y5) , the expected number of for months in which the unemployment rate is price is 5 percent.Report the upper bound for the interval.
The slope term (b) in the estimated regression equation is -8.The intercept term (a) is 237.Construct a 95% confidence interval estimate of E(y5) , the expected number of for months in which the unemployment rate is price is 5 percent.Report the upper bound for the interval.
A) 326.4
B) 205.7
C) 289.3
D) 227.5
E) 301.6
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Suppose a rental car company uses simple linear regression to develop an equation that predicts the repair costs for each of its vehicles based on the mileage of the car (total miles driven) .The company uses the following data on repair costs and miles driven for five of its cars:  The least squares line predicts that if the mileage of a car increases by 10,000 miles, its annual repair costs will increase by an estimated:
The least squares line predicts that if the mileage of a car increases by 10,000 miles, its annual repair costs will increase by an estimated:
A) $13.85
B) $64.64
C) $138.52
D) $144.96
F) C) and D)
Correct Answer

verified
Correct Answer
verified
True/False
A procedure used for finding the equation of a straight line that provides the best fit by minimizing the sum of the squared vertical distances of points from the line is called the least squares method.
B) False
Correct Answer

verified
Correct Answer
verified
Showing 101 - 111 of 111
Related Exams